Ukázka je z knihy Meteorologie (J. Bednář, 2003).

16.1  Index lomu, základní zákony odrazu a lomu světelných paprsků

Na obr. 16.1 máme znázorněn světelný paprsek, který v bodě A dopadá z prostředí 1 na rozhraní, částečně je odrážen zpět do prostředí 1 a částečně se lomí do prostředí 2. Symboly a , a ', b značíme po řadě úhel dopadu, úhel odrazu a úhel lomu uvažovaného paprsku. Kromě právě zmíněného paprsku si povšimněme paprsku s ním rovnoběžného, jenž v bodě B dopadá na dané rozhraní, a jako bod C označme průsečík tohoto druhého paprsku s rovinou k němu kolmou a procházející bodem A. Podobně označme D průsečík lomeného paprsku s rovinou k němu kolmou a obsahující bod B. Prvá ze zmíněných rovin vyznačených na obr. 16.1 přerušovanými čarami představuje vlnoplochu příslušející elektromagnetickému vlnění vytvářejícímu svazek rovnoběžných paprsků dopadajících na uvažované rozhraní v okamžiku, kdy prvý z vyznačených dvou paprsků dosáhne bodu A, zatímco druhá odpovídá vlnoploše příslušející lomeným paprskům v okamžiku, kdy druhý paprsek se právě částečně odráží a lomí v bodě B. Z triviálních vlastností vlnoploch je okamžitě zřejmé, že čas t potřebný na to, aby světelný paprsek urazil v prostředí 1 dráhový úsek CB, musí být roven času, za který lomený paprsek proběhne v prostředí 2 dráhu délky AD. To však znamená

když v₁, resp. v₂ značí rychlost světelných paprsků v prostředí 1, resp. 2. Odtud dostáváme

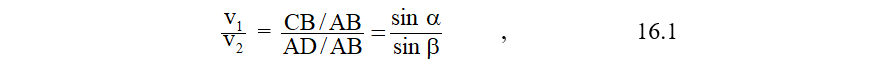
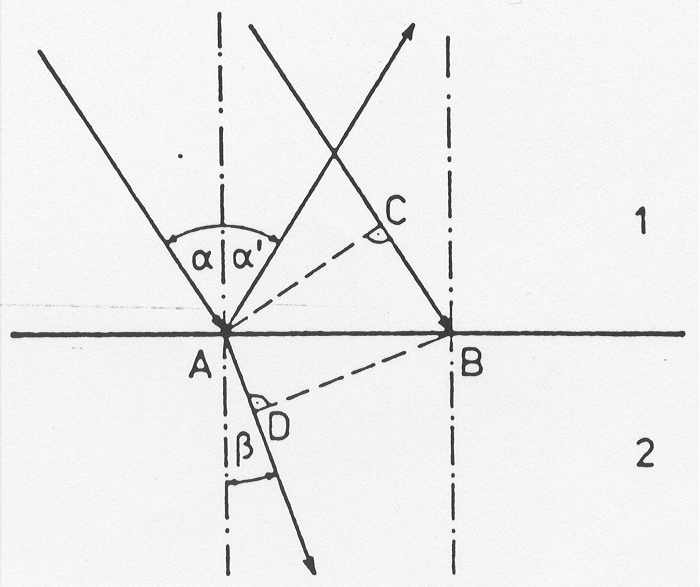
což vyjadřuje základní zákon lomu světelných (elektromagnetických) paprsků, jenž se označuje jako Snellův zákon.

Box 14: Optické jevy a inspirace lidské mysli
Optické jevy v atmosféře patří k nejznámějším a nejpůsobivějším přírodním úkazům. Není proto divu, že odedávna upoutávaly pozornost člověka, což se výrazně projevuje v různých mýtech, ale i v záznamech kronik. Výjimkou v tomto směru není ani bible, kde např. v 1. knize Mojžíšově nalézáme v souvislosti s Noemovou obětí pasáž o duze jako o znamení smíru (Gen 9, 12n.) po potopě světa.
"Toto je znamení smlouvy, jež kladu mezi sebe a vás i každého živého tvora, který je s vámi, pro pokolení všech věků: Položil jsem na oblak duhu, aby byla znamením smlouvy mezi mnou a zemí. Kdykoli zahalím zemi oblakem a na oblaku se ukáže duha, rozpomenu se na svou smlouvu mezi mnou a vámi i veškerým živým tvorstvem, a vody již nikdy nezpůsobí potopu ke zkáze všeho tvorstva."
Ve vidění proroka Ezechiela ve stejnojmenné starozákonní knize nalézáme popisy, které nápadně připomínají některé halové jevy (Ez 1, 15n.):
"Když jsem na ty bytosti hleděl, hle, na zemi u těch bytostí, před každou z těch čtyř, bylo po jednom kole. Vzhled a vybavení kol bylo toto: třpytila se jako chryzolit a všechna čtyři se sobě podobala; jejich vzhled a vybavení se jevilo tak, jako by bylo kolo uvnitř kola. ... Když se bytosti pohybovaly, pohybovala se s nimi i kola, a když se bytosti vznášely nad zemí, vznášela se i kola."

Obr. 16.1: Ilustrace k výkladu zákonů odrazu a lomu

Spolu s lomem (refrakcí) světelných paprsků dochází na uvažovaném rozhraní k jejich částečnému odrazu (reflexi). Tento odraz se řídí následujícími dvěma zákony:

1. Odražený paprsek zůstává v rovině dopadu určené dopadajícím paprskem a kolmicí k uvažovanému rozhraní v bodě dopadu daného paprsku. Stejný zákon platí i pro paprsek lomený do druhého prostředí.
   
   
2. Úhel odrazu se rovná úhlu dopadu, tj. na obr. 16.1 a '=a .

V případě v₁ > v₂ se paprsek lomí z prostředí opticky řidšího do prostředí opticky hustšího a podle (16.1) musí platit a > b (lom ke kolmici), což vidíme zakresleno na obr. 16.1. V opačném případě, kdy v₁ < v₂, se jedná o lom od kolmice (a <b ) a paprsek se šíří z prostředí opticky hustšího do prostředí opticky řidšího. Ve druhém z právě uvedených dvou případů existuje mezní úhel dopadu a ^* , při němž lomený paprsek směřuje rovnoběžně s rovinným rozhraním a za situace, kdy úhel dopadu a > a ^* , dochází k totálnímu odrazu, při němž žádný lom do opticky řidšího prostředí nevzniká. Hodnota a ^* závisí na relativním indexu lomu (viz dále) daných dvou prostředí a určíme ji z (16.1), dosadíme-li za b pravý úhel.

Jestliže jako prvé prostředí uvažujeme vakuum, potom zavedeme

kde v značí rychlost šíření světelných (obecně elektromagnetických) paprsků v daném prostředí (v našem případě prostředí 2) a c je rychlost těchto paprsků ve vakuu. Veličina n se pak nazývá absolutní index lomu tohoto prostředí. Máme-li dvě prostředí[4] o absolutních indexech lomu n₁ a n₂, potom zřejmě pro relativní index lomu n₂₁ druhého prostředí vůči prvnímu platí

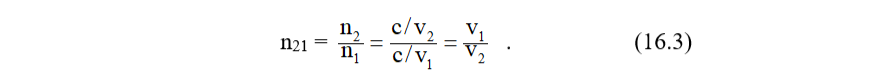
Absolutní index lomu vzduchu se poněkud zvětšuje s klesající vlnovou délkou elektromagnetického záření, což názorně ukazuje tab. 16.1.

Tab. 16.1: Závislost absolutního indexu lomu vzduchu n pro část oboru viditelného elektromagnetického záření o vlnové délce l

16.2  Lom (refrakce) světelných paprsků v atmosféře

Absolutní index lomu n pro elektricky nevodivá prostředí je obecně dán vztahem

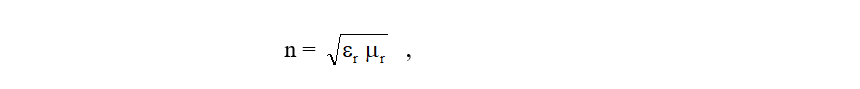
jenž vyplývá ze základů teorie elektromagnetického záření a kde e _r je relativní elektrická permitivita a ľ _r relativní magnetická permeabilita daného prostředí. Elektrická vodivost vzduchu v troposféře a stratosféře je natolik malá, že tento vztah zde můžeme pro elektromagnetické paprsky plně aplikovat, a navíc, vzhledem k tomu, že pro vzduch je ľ _r prakticky rovno jedné, jej můžeme zjednodušit do tvaru

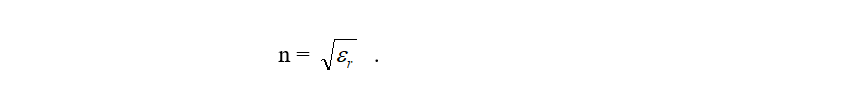
V oboru viditelného elektromagnetického záření lze využít též vztahu

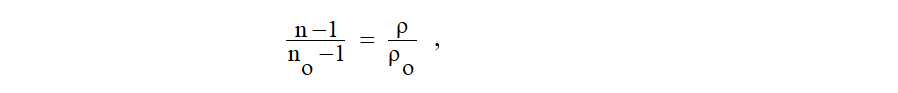
v němž r značí hustotu vzduchu, jíž odpovídá index lomu n, a n₀ je index lomu při konvenčně stanovené počáteční (standardní, normální) hustotě vzduchu r ₀. Za r ₀ obvykle volíme hustotu suchého vzduchu při tlaku 1000 hPa a teplotě 0 ^°C .

Z naposled uvedeného vztahu vyplývá, že index lomu, tj. optická hustota prostředí, roste se zvětšující se hustotou vzduchu. Za běžného stavu v atmosféře, kdy hustota vzduchu klesá s výškou, se tedy paprsek vyslaný ze zemského povrchu šikmo vzhůru láme od kolmice (viz obr. 16.2a), tj. je zakřiven ve smyslu odpovídajícím zakřivení zemského povrchu. Paprsek šířící se atmosférou šikmo dolů je zakřiven ve stejném smyslu, tj. láme se ke kolmici.

---

Obr. 16.2: Zakřivení světelného paprsku v atmosféře; a) při poklesu hustoty vzduchu s výškou, b) v anomálním případě inverze hustoty vzduchu

---

V atmosféře, a to zpravidla v relativně tenké vzduchové vrstvě nad zemským povrchem silně ohřátým slunečním zářením, však může vzniknout anomální situace, kdy hustota vzduchu s výškou roste. Tento případ vzniká tehdy, jestliže teplota vzduchu klesá s výškou rychleji než o 0,0342 K m^-1, což je velmi silně instabilní stav. Potom nastávají z hlediska lomu světelných paprsků případy, kdy paprsek šířící se ovzduším šikmo vzhůru se láme ke kolmici (viz obr. 16.2b) a paprsek postupující šikmo shora dolů od kolmice. Zakřivení paprsků má potom opačný smysl vzhledem k zakřivení zemského povrchu.

S právě popsaným lomem světelných paprsků v atmosféře souvisí řada optických jevů, z nichž k nejznámějším patří astronomická refrakce, zelený záblesk, různé typy zrcadlení a zvednutí či snížení obzoru. Budeme se jim nyní věnovat podrobněji.

16.3  Astronomická refrakce

Jako astronomickou refrakci označujeme celkové stočení trajektorie světelného paprsku způsobené jeho lomem od vstupu shora do zemské atmosféry až po úroveň zemského povrchu. Pozorovatel nalézající se na zemském povrchu v bodě P (viz obr. 16.3) nechť sleduje např. určitou hvězdu, která by se při neexistenci lomu světelných paprsků v atmosféře nacházela na nebeské klenbě v bodě A. Světelný paprsek procházející ovzduším shora dolů však postupuje do stále hustších vzduchových vrstev, a lomí se proto ke kolmici. Pozorovatel potom vnímá danou hvězdu ve směru tečny vedené k zakřivenému paprsku v bodě, kde tento paprsek vstupuje do jeho oka, tj. na obr. 16.3 ve směru od bodu P do bodu A'.

---

Obr. 16.3: Astronomická refrakce

---

Velikost astronomické refrakce výrazně závisí na délce dráhy paprsku v zemské atmosféře, tj. na výšce pozorovaného objektu nalézajícího se mimo ovzduší (např. hvězdy, Slunce, Měsíce) nad obzorem. Pro zenit je zřejmě nulová, u obzoru dosahuje přes polovinu úhlového stupně. Přesná hodnota však závisí i na konkrétním prostorovém rozložení hustoty vzduchu v daném případě.

Analogickým jevem je zemská refrakce definovaná inverzně jako celkový úhel stočení trajektorie paprsku vycházejícího se zemského povrchu a procházejícího atmosférou šikmo vzhůru do kosmického prostoru.

Obdobným úkazem, avšak v podstatně menším prostorovém měřítku, je boční refrakce působená lomem přibližně horizontálních světelných paprsků na nehomogenitách hustoty vzduchu, vznikajících nejčastěji následkem intenzivního nerovnoměrného zahřívání zemského povrchu slunečním zářením během denních hodin. Tento jev působí např. obtíže při geodetických pracích v terénu.

16.4  Zelený záblesk

Protože index lomu obecně závisí na vlnové délce elektromagnetického záření, což dokumentuje uvedená tab. 16.1, jeví světelné paprsky tvořené nemonochromatickým zářením při lomu disperzi. Velikost indexu lomu roste s klesající vlnovou délkou, což znamená, že astronomická, zemská, popř. boční refrakce bude o něco větší pro krátké vlnové délky z modrofialového konce spektra viditelného záření než pro větší vlnové délky z červeného konce.

Vezměme si paprsek, který vstoupil z kosmu do zemské atmosféry a prochází jí šikmo k zemskému povrchu. Představme si, že např. jde o paprsek přímého slunečního záření, a omezíme-li se pouze na jeho viditelnou složku, je astronomická refrakce největší pro fialovou, dále modrou a zelenou část spektra a nejmenší pro část červenou. Uvědomíme-li si, že v důsledku astronomické refrakce vnímáme sluneční disk o něco výše nad obzorem, než odpovídá jeho skutečné poloze, je zřejmé, že při západu Slunce (a analogicky i při jeho východu) nastává situace, kdy větší vlnové délky z červeného konce spektra jsou již (ještě) "zapadlé" za obzorem, zatímco zelenou, modrou a fialovou barvu lze ještě (již) po několik sekund vnímat.

V případě čisté atmosféry (velmi malého zakalení vzduchu prachovými částicemi, vodními kapičkami nebo ledovými krystalky) můžeme někdy sledovat optický úkaz nazývaný zelený záblesk, popř. zelený paprsek, kdy sluneční disk ve chvíli svého západu na okamžik zazáří nazelenalým světlem. Na prvý pohled by se mohlo zdát podivné, že se neobjevuje spíše záblesk modrý nebo fialový, avšak nejkratší vlnové délky světla (fialová a modrá barva) jsou velmi účinně rozptylovány molekulami vzduchu. Modrý záblesk v okamžiku západu Slunce je proto jevem zcela výjimečným.

Stejným způsobem lze snadno vysvětlit i laminaci slunečního disku při jeho poloze v bezprostřední blízkosti obzoru. Jeho dolní část bývá zbarvena sytě červeně, tato barva směrem vzhůru pak přechází v oranžovou, žlutou, někdy až nazelenalou na horním okraji.

16.5  Zvednutí obzoru

V běžných případech, kdy hustota vzduchu klesá v atmosféře s výškou, se světelné paprsky procházející šikmo ovzduším zakřivují v důsledku lomu ve stejném smyslu, jako je zakřiven zemský povrch. Paprsky pak pronikají i poněkud za obzor a dochází tak k jeho zdánlivému zvednutí, což je názorně patrné z obr. 16.4. Pozorovatel v bodě P vnímá objekt A ve směru tečny k paprsku, jenž od tohoto objektu přichází do jeho oka, tj. vidí daný objekt posunutý poněkud vzhůru do bodu A'. Právě zmíněné zvednutí obzoru je tím výraznější, čím rychleji klesá hustota vzduchu s výškou. Zvláště příznivé podmínky pro jeho pozorování se vyskytují za situací s mohutnými přízemními inverzemi teploty, kdy se u zemského povrchu nalézá relativně těžký studený vzduch, zatímco teplota roste s výškou, a hustota vzduchu směrem vzhůru proto klesá relativně velmi rychle.

---

Obr. 16.4: Zvednutí obzoru

---

16.6  Zrcadlení v atmosféře

Jedním z nejatraktivnějších optických jevů v atmosféře je svrchní (horní) zrcadlení. Vznik tohoto úkazu schematicky znázorňuje obr. 16.5. Povšimněme si nejprve světelného paprsku 1, který z místa A postupuje atmosférou šikmo vzhůru, přičemž dochází k lomu od kolmice (následek poklesu hustoty vzduchu a tím i absolutního indexu lomu s výškou). V případech, kdy hustota vzduchu klesá s výškou zvláště rychle, což je typické zejména pro vrstvy s teplotními inverzemi (vrstvy I a II na obr. 16.5), může úhel dopadu, tj. úhel sevřený paprskem a vertikálou, nabýt kritické hodnoty pro totální odraz a takovou situaci máme na uvažovaném paprsku znázorněnu v bodě C₁. Paprsek se potom ohne zpět k zemskému povrchu a na svém dalším postupu prochází stále hustšími vrstvami vzduchu, lomí se tedy ke kolmici, až se v místě B dostává do oka pozorovatele. Z bodu B pak lze ve směru tečny k paprsku 1, která na obr. 16.5 směřuje k bodu A', spatřit převrácený obraz situace v místě A, jež se může nalézat za obzorem.

---

Obr. 16.5: Svrchní (horní) zrcadlení

---

V případě, kdy v atmosféře existuje více vrstev s teplotní inverzí nad sebou, může dojít k úkazu, při němž lze pozorovat vícenásobně svrchní zrcadlení (dva nebo i více obrazů vzdálených objektů nad sebou). Schematické znázornění opět vidíme na obr. 16.5, uvažujeme-li kromě paprsku 1 i zakreslený paprsek 2, který je totálně odrážen v bodě C₂ na teplotní inverzi II a vytváří pozorovateli nalézajícímu se v bodě B zdánlivý převrácený obraz místa A znázorněný jako A''.

Vznik právě popsaného úkazu svrchního zrcadlení je typický pro geografické oblasti vyznačující se výskytem mohutných výškových inverzí teploty. Patří sem především polární oblasti a v některých případech oblasti suchých tropických pásů (pouští). Ve druhém z těchto případů však vlastní jev svrchního zrcadlení může být kombinován se spodním zrcadlením (viz dále) v silně přehřáté přízemní vrstvě vzduchu, což má za následek, že zdánlivý obraz vzdálených objektů vidíme nepřevrácený a těsně při obzoru (ve skutečnosti znovu převrácený do přirozené polohy). U nás je svrchní zrcadlení poměrně řídkým jevem, a pokud se vyskytne, bývá to zpravidla v zimním období, neboť v chladné části roku jsou v našich oblastech podstatně příznivější podmínky pro vytváření mohutných teplotních inverzí než v létě.

---

Obr. 16.6: Spodní zrcadlení

---

Při velmi intenzivním ohřívání zemského povrchu slunečním zářením však někdy vzniká situace, za níž v přehřáté přízemní vrstvě vzduchu, silné několik centimetrů až několik metrů, hustota vzduchu s výškou roste, což se stává, klesá-li teplota vzduchu s vertikální souřadnicí rychleji než o 0,0342 K m ^{- 1}. V souvislosti s tím si na obr. 16.6 povšimněme světelného paprsku, který vychází z objektu A a postupuje přehřátou přízemní vrstvou (s anomálním vertikálním růstem hustoty vzduchu) do naznačeného oka pozorovatele P. V tomto případě se uvažovaný paprsek nejprve lomí od kolmice, jeho úhel dopadu roste, až v bodě O dosáhne kritické hodnoty potřebné pro totální odraz, paprsek se ohýbá směrem vzhůru a začne se lámat ke kolmici. Pozorovatel P pak ve směru tečny vedené ze svého oka k danému paprsku vidí zrcadlově převrácený obraz objektu A. Takto popsaný jev, tzv. spodní zrcadlení, je typickým úkazem zejména v horkých pouštích, ale vyskytuje se zcela běžně i u nás, a to především nad sluncem rozpálenými betonovými nebo asfaltovými plochami.

V případě, že se pozorovatel na obr. 16.6 nalézá mezi objektem A a bodem totálního odrazu O, nepozoruje spodní zrcadlení, avšak objekt A se mu jeví nepřevrácený poněkud níže, než se ve skutečnosti nalézá. Tímto způsobem vzniká tzv. snížení obzoru.

V souvislosti s optickými přeludy vytvářenými v atmosféře svrchním a spodním zrcadlením, popř. jejich kombinací, se často používá název fata morgána, který však nemá charakter striktně odborného termínu. V původním smyslu jde, dle literárních pramenů, o staré lidové označení klamných obrazů v ovzduší pocházející z oblasti Messinské úžiny.

16.7  Optické jevy vznikající ohybem světelných paprsků na vodních kapičkách

Tyto jevy popíšeme a stručně vysvětlíme v následujícím přehledu.

Koróna

Jde o optický jev vznikající ohybem světla na konturách vodních kapiček v oblacích, mlhách nebo kapiček volně rozptýlených v ovzduší v podobě tzv. kouřma. Je tvořen jedním nebo více sledy soustředných kruhových barevných prstenců těsně kolem Slunce, popř. Měsíce. V každém sledu je na vnitřní straně fialová nebo modrá barva, zatímco vnější kruh je červený; mezi tím se vyskytují ostatní barvy spektra. Výraznost a jasnost barev je největší, mají-li zmíněné vodní kapičky vzájemně stejné poloměry. Není-li splněna tato podmínka, barvy se rozostřují, v případě větší rozmanitosti velikostí kapek má koróna vzhled pouze bělavého, popř. velmi mdle zbarveného kruhu kolem okraje slunečního nebo měsíčního disku. V této podobě bývá velmi často pozorována v noci kolem Měsíce (lidově tzv. studánka). Obdobný jev lze pozorovat v případě vzdálených bodových pozemských zdrojů světla. Laboratorně můžeme analogický jev realizovat ohybem světelných paprsků na kruhových terčících nebo otvorech.

Glórie

Koróně analogický optický jev v podobě jednoho nebo více sledů barev spektra v podobě kruhů kolem stínu vrženého na vrstvu oblaku nebo mlhy obsahující vodní kapičky, někdy i kolem stínu vrženého na soubory kapek rosy. Vzniká zpětným rozptylem světla na sférických vodních kapičkách, což lze kvantitativně popsat např. prostřednictvím Mieovy teorie rozptylu elektromagnetického záření. Jestliže je zmíněná vrstva oblaku nebo mlhy velmi blízko předmětu vrhajícího stín, popř. se tento předmět nalézá uvnitř ní (typicky na horách), zdá se stín velmi zvětšený a jev pak bývá lidově označován jako tzv. horský nebo brockenský přízrak (strašidlo). Barevná výraznost glórie je relativně nejlepší, jestliže rozptylující vodní kapičky jsou si vzájemně velikostí co nejbližší, obecně však bývá celý jev výrazně slabší ve srovnání s korónou.

Iridescence, irizace

Iridescence (irizace) je barevné, často proměnlivé zabarvení okrajů, popř. průsvitných částí oblaků ve slunečním záření, popř. měsíčním světle. Jde o ohybový jev na vodních kapičkách přítomných v oblaku, tj. v podstatě o rozostřenou a prostorově roztaženou korónu při prostorově silně nehomogenní koncentraci vodních kapiček. Typicky se vyskytuje např. u oblaků druhu cirrocumulus a altocumulus.

Perleťové oblaky

Označují se tak oblaky ve výškách asi 20--30 km, podobající se tvarově oblakům druhu cirrus nebo čočkovitým oblakům druhu altocumulus, na nichž se výrazně projevuje iridescence, čímž nabývají vzhledu perleti. Jsou pozorovány při výškách Slunce několik stupňů pod obzorem, tzn. zejména večer nebo ráno, ve vyšších zeměpisných šířkách i po celou noc. Na základě výrazné iridescence se předpokládá, že jsou složeny převážně z malých, silně přechlazených vodních kapiček. Jsou často pozorovány např. v oblasti jižní Skandinávie.

Od perleťových oblaků je třeba odlišovat noční svítící oblaky (stříbřité oblaky), což jsou velmi tenké oblaky ve výškách asi 70--90 km, projevující se stříbřitě šedým světélkováním na tmavém pozadí noční oblohy. Jde o poměrně vzácný jev a pro jejich vysvětlení existují dvě hypotézy. První předpokládá, že jde o shluky částic zejména vulkanického nebo kosmického prachu, druhá se zakládá na předpokladu, že jsou tvořeny soubory drobných ledových částeček vzniklých z vodní páry, která se v těchto výškách vytvořila fotochemickou syntézou z kyslíku a vodíku. Výskyt tohoto jevu bývá pozorován ve středních a vyšších zeměpisných šířkách v letních měsících při polohách Slunce asi 5--13 stupňů pod obzorem.